
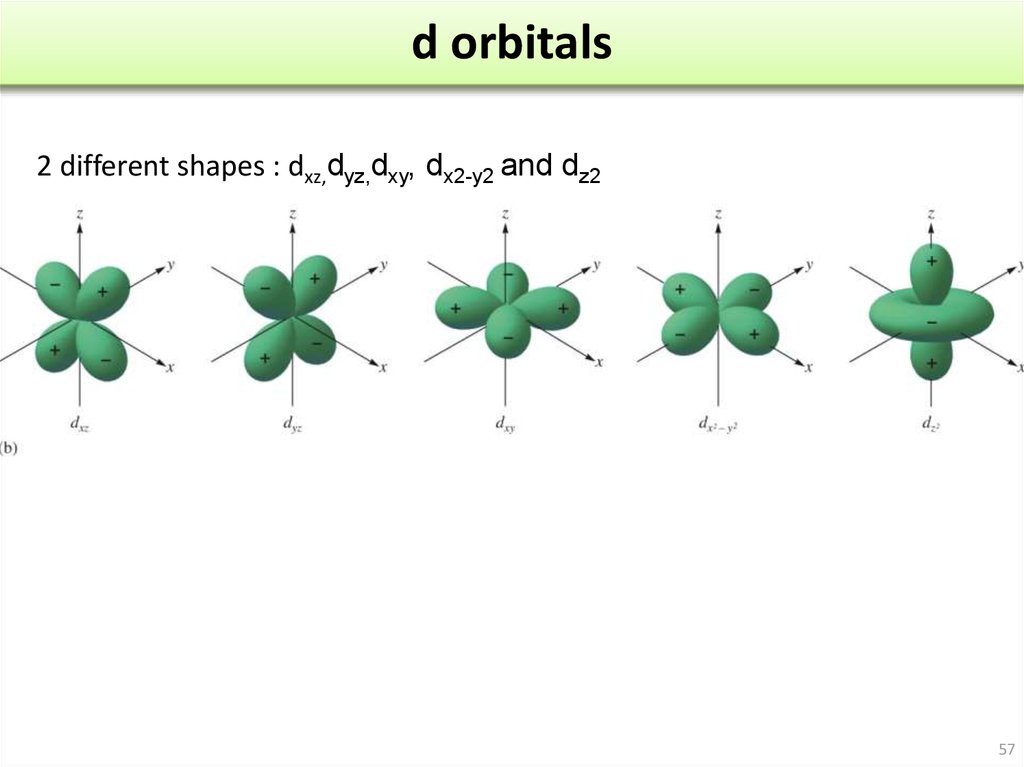
have angular momentum and stay away from the nucleus. These antinodes are found only in the s orbitals as all the other orbitals p,d,f, etc. This looks like a solid ball.īut for n = 2 or more, there are spherically symmetrical shells which means that there is a radial wave-structure with a sinusoidal radial component.Īn antinode can be observed at the centre of the nucleus in s orbitals irrespective of their n numbers. The density of electrons is seen the most near the centre of the atom, and the density reduces as we move away from the nucleus. The s-orbitals are of spherical shape as the quantum number l = 0. But if the orbital is shown by the equations of complex numbers then the quantum number “m” will show the shape or orbital. The shape of orbitals is determined by the quantum number “l”, and the quantum number “m” determines its orientation. Shapes of orbitalĮach orbital has a different type of 3-dimensional shape. This formula is also applicable to an unstable atom.Īs there is no certainty of an electron's position, the orbitals are the spaces where the electrons are most likely to be present or are the site of maximum probability of the location of electrons in an atom.
So, when the uncertainties in momentum and position of a particle are multiplied, it is ≥ h/4pi. The uncertainty principle uses the momentum and position factor of a particle, where the momentum is equal to the mass multiplied by the velocity. Thus, the uncertainty principle is relevant only for the objects with small sizes like an atom. This is because the uncertainty, in this case, is too small. But we can easily calculate the position and velocity of a car. The Heisenberg uncertainty principle actually said that for any object in the universe, both the exact position and the exact velocity can not be calculated at the same time even in theory. So, the orbitals actually show the shape of the region where an electron can be found 95% of the time. From this, we can say that it is not possible to calculate the position and momentum of an electron with absolute precision. The Heisenberg Uncertainty Principle says that it is not possible to find the current position of an electron and its position an instant later. The s orbital has the lowest energy as it is closest to the nucleus while the d orbital has the maximum energy as it is farthest from the nucleus. They are the s orbital, p orbital, d orbital, and f orbital. Their movement is subjected to quantum mechanics, and it is described using 3-dimensional clouds known as orbitals.Ī total of four different orbitals have been discovered to date. Unlike the fixed-orbit path of planets around the sun, electrons present in an atom don't follow a definite path. How many electrons can be accommodated in different orbitals?Īccording to atomic theory and quantum mechanics, an atomic orbital is a mathematical expression that presents the wave-like behaviour of 1 or 2 electrons of an atom.What are the different atomic orbitals?.Zimmerman, Nuovo Cimento B 62, 91 (1981). 26, 565 (1978) Google Scholar CrossrefĪnd Collective Field Theory of Superliquid 3 He, Berlin preprint FUB‐HEP 14/78, extended version of Erice Lecture Note (1978) edited by A. Popov, CERN preprint TH 2424 (1977) Google ScholarĪnd Functional Integrals in Quantum Field Theory and Statistical Physics (Atomizdat, Moscow, 1976) Google Scholar

This is not a true “measure” in the classical sense of theory of integration. Runge, Vectoranalysis (Hirzel, Leipzig, 1919), Vol. For continuum states, it turns out that the dynamical symmetry group is isomorphic to the group of Lorenz transformations in one time and three space dimensions rather than to the group of rotations in four space dimensions. We implicitly are restricting our considerations on the 0 (4) generators to bound states. The geometrical symmetry we are considering should be distinguished from the dynamical symmetries that lead to the unexpected degeneracies of the energy levels of the hydrogen atom and the isotropic harmonic oscillator. Chlsholm, Croup Theoretical Techniques in Quantum Chemistry (Academic, New York, 1976). Keyman, Current ICTP IC/80/129, preprint, Miramare, Triestre (1980). Hibbs, Quantum Mechanics and Path Integrals (McGraw‐Hill, New York, 1965).


 0 kommentar(er)
0 kommentar(er)
